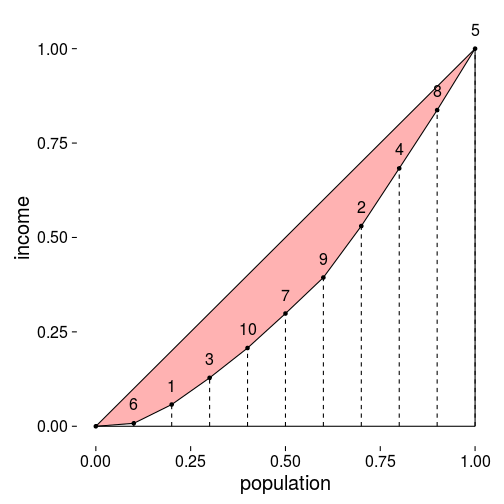
与Lorenz曲线相关的指标

15 Jul 2016

在前面一篇博客“对加权Gini系数的理解”中，我们已经对Lorenz曲线的构造方法进行了探讨，当时的主要目的是计算加权Gini系数。事实上，Gini系数并不能表现出Lorenz曲线的全部信息，因为同一个Gini系数可能对应不同的Lorenz曲线。为了进一步挖掘Lorenz曲线的信息，Damgaard等人¹提出了Lorenz不对称系数，用来说明不公平性到底是由于低收入的人群占比太高导致的，还是由于少量人群占据了大量的收入所致。另外，学者还提出了Hoover指数(或者称为Ricci-Schutz系数以及Robin Hood指数)，用来分析到底有多大比例的收入需要再分配才能实现“绝对公平”。由于Hoover指数相对比较简单，这里先探讨Hoover指数，然后再对Lorenz不对称系数进行说明。

1 Hoover指数

Hoover指数的想法是十分简单的，假设有$n$个人的收入分别为$x_1,x_2,\cdots,x_n$，其平均数为$\bar{x}$，考虑到最公平的分配方式是这$n$个人的收入都是$\bar{x}$，那么每个人的缺口就是$\|x_i-\bar{x}\|$。这时我们可以计算出总的缺口占总收入的比例：

$$\text{HI}=\dfrac{\sum_{i=1}^n\|x_i-\bar{x}\|}{2\sum_{i=1}^n{x_i}}$$

这个比例就是Hoover指数。在Hoover指数的计算公式中需要除以$2$，其原因是$x_i-\bar{x}<0$的$\|x_i-\bar{x}\|$的总和与$x_i-\bar{x}>0$的$\|x_i-\bar{x}\|$的总和相等，也就是说高于平均收入的人群需要拿出的收入的总和等于低于平均收入的人群需要获得的收入的总和时才能实现“绝对公平”。按照这种方式，我们很容易就能计算出“对加权Gini系数的理解”中第一个表格中数据的Hoover指数，其结果为 $0.206$。

对加权Gini系数的理解

12 Jul 2016

1 Gini系数

Gini系数是研究不公平性(或者说公平性)的一个重要指标。它的计算可以通过Lorenz曲线来实现。假如我们研究一个群体内部收入分配的公平性问题，那么首先可以刻画这个群体内部收入分配的Lorenz曲线，具体方式如下：假设这个群体内部共有$n$个人，每个人的收入分别为$x_1,x_2,\cdots,x_n$，然后我们可以对这$n$个人的收入按照从小到大的顺序进行排序，得到$x_１^\prime,x_2^\prime,\cdots,x_n^\prime$，这时我们可以构造一组坐标$(h/n,L_h/L_n)$，这里$h=0,1,\cdots,n$，$L_0=0$，$L_h=\sum_{i=0}^hx_i^\prime$。我们将这些坐标点绘制在平面直角坐标系中并依次相连，所得到的曲线就是Lorenz曲线。为了说明这一过程，假设$n=10$，具体的收入状况如下表所示：

id	income
1	28.76
2	78.83
3	40.90
4	88.30
5	94.05
6	4.56
7	52.81
8	89.24
9	55.14
10	45.66

绘制的Lorenz曲线如下：