对加权Gini系数的理解

12 Jul 2016

1 Gini系数

Gini系数是研究不公平性(或者说公平性)的一个重要指标。它的计算可以通过Lorenz曲线来实现。假如我们研究一个群体内部收入分配的公平性问题，那么首先可以刻画这个群体内部收入分配的Lorenz曲线，具体方式如下：假设这个群体内部共有$n$个人，每个人的收入分别为$x_1,x_2,\cdots,x_n$，然后我们可以对这$n$个人的收入按照从小到大的顺序进行排序，得到$x_１^\prime,x_2^\prime,\cdots,x_n^\prime$，这时我们可以构造一组坐标$(h/n,L_h/L_n)$，这里$h=0,1,\cdots,n$，$L_0=0$，$L_h=\sum_{i=0}^hx_i^\prime$。我们将这些坐标点绘制在平面直角坐标系中并依次相连，所得到的曲线就是Lorenz曲线。为了说明这一过程，假设$n=10$，具体的收入状况如下表所示：

id	income
1	28.76
2	78.83
3	40.90
4	88.30
5	94.05
6	4.56
7	52.81
8	89.24
9	55.14
10	45.66

绘制的Lorenz曲线如下：

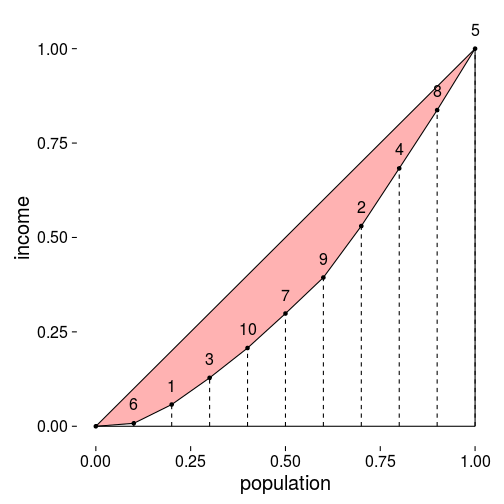
上图中红色部分的面积占整个下三角区域面积的比例即为Gini系数。为了计算这个Gini系数，我们对Lorenz曲线上每个点向下引一条垂线，这样就可以将Lorenz曲线与x轴围城的区域划分成很多个梯形区域(其中第一个区域为三角形区域)，那么我们就能够对这些区域的面积进行计算。假设Lorenz曲线上的任意一点为$(X_i,Y_i)$(这里$i=0,1,\cdots,n$，$X_0=0$，$Y_0=0$)，那么该点与前一个点形成的梯形区域的面积为$(X_i-X_{i-1})(Y_i+Y_{i-1})/2$，整个面积为$\sum_{i=1}^n(X_i-X_{i-1})(Y_i+Y_{i-1})/2$。显然下三角区域的面积为$1/2$，那么Gini系数的计算公式如下：

$$\text{Gini}=1-\sum_{i=1}^n(X_i-X_{i-1})(Y_i+Y_{i-1})$$

对于以上算例，根据公式计算出来的Gini系数的结果为$0.2711$。

2 对Lorenz曲线的认识

Lorenz曲线到底是怎样一种曲线？从前面的分析中我们知道，只要我们给出一列数据(如$x_1,x_2,\cdots,x_n$)，我们就能生成一批Lorenz曲线上的坐标点$(X_i,Y_i)$(这里$i=0,1,\cdots,n$)。可见，Lorenz曲线上的坐标点与原始数据存在着一定的函数关系，假设这种函数关系为$(F(x),L(x))$，对于系列中任意一个数据$x_i$，其对应的Lorenz曲线上的坐标为$(F(x_i),L(x_i))$。那么，$F(x)$和$L(x)$分别代表什么呢？事实上，$F(x)$是$x$的累积经验分布函数。在前面的算例中，其形式如下：

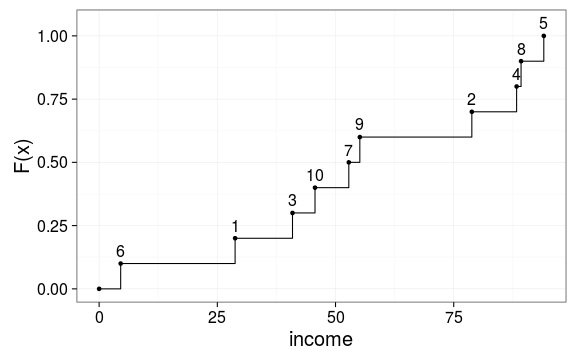
而$L(x)$则为将$x$进行从小到大排序后依次累积加所得到的值，其形式如下：

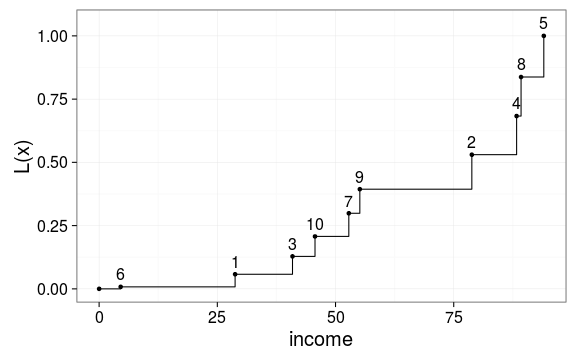
这样，我们将对应点上的坐标提取出来就可以得到这样一个三元组$(x,F(x),L(x))$。同样，原则上我们也可以得到任意一个$x$所对应的Lorenz曲线上的点$(F(x),L(x))$，比如$x$的期望值$\mu$对应的Lorenz曲线上的点为$(F(\mu),L(\mu))$。

事实上，$F(x)$和$L(x)$存在一定的联系，这种联系可以用以下表达式来说明：

$$\begin{cases} F(x)=\int_{0}^{x}\text{d}F(t)\\ L(x)=\int_{0}^{x}t\text{d}F(t)/\int_{0}^{+\infty}t\text{d}F(t) \end{cases}$$

这里$F(0)=0$。$L(x)$实际上就是不大于$x$那部分数据加权和占所有数据加权和的比例，其中$\text{d}F(x)$就是权重。

3 加权Gini系数

在实际情况中，我们往往只知道一个团体总的收入状况和团体的人口数，而不知道团体内部每个人的收入状况。在我们分析所有团体的收入分配公平性问题时，一个十分必要的假设就是在每个团体内部收入分配是完全公平的(即按人口平均分配)。为了说明加权Gini系数的计算过程，同样我们也可以假设以下数据：

group_id	total_income	population
1	89.55	8
2	210.51	5
3	732.96	13
4	852.13	16
5	788.40	9
6	331.96	14
7	82.43	11
8	285.53	6
9	237.50	18
10	385.24	4

按照Gini系数的定义，我们首先还是得刻画Lorenz曲线，即确定函数$F(x)$和$L(x)$。需要明确的是$x$的含义，我们的任务不是分析不同团体总收入的分配公平性问题，而是不同团体中每个人的收入的分配公平性问题，那么$x$表示的不是团体总收入，而是团体的人均收入。假设第$i$个团体总收入为$z_i$，其人口数为$w_i$，那么人均收入$x_i=z_i/w_i$。为了计算$F(x)$，我们先对$x_i$按照从小到大的顺序进行排序，得到$x_１^\prime,x_2^\prime,\cdots,x_n^\prime$，并且令$x_0^\prime=0$，$F(x_0^\prime)=0$和$L(x_0^\prime)=0$。这样同时可以得到$z_i$和$w_i$的排序值$z_i^\prime$和$w_i^\prime$。那么，我们很容易得到

$$\begin{cases} F(x_{h}^{\prime}) & =\sum_{i=0}^{h}w_{i}^{\prime}/\sum_{i=0}^{n}w_{i}^{\prime}\\ L(x_{h}^{\prime}) & =\sum_{i=0}^{h}w_{i}^{\prime}x_{i}^{\prime}/\sum_{i=0}^{n}w_{i}^{\prime}x_{i}^{\prime}\\ & =\sum_{i=0}^{h}z_{i}^{\prime}/\sum_{i=0}^{n}z_{i}^{\prime} \end{cases}$$

这里$h=0,1,\cdots,n$。这时绘制出来的Lorenz曲线如下所示：

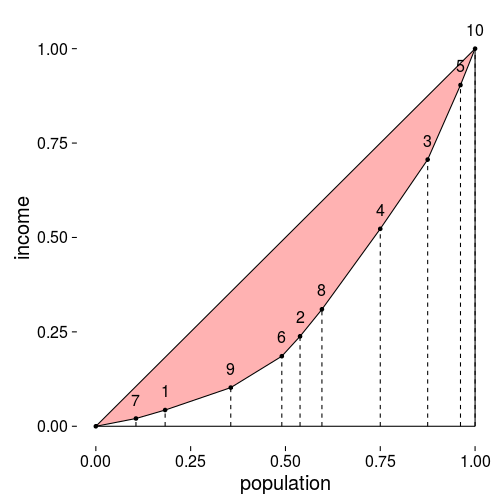
计算出来的Gini系数的结果为$0.3827$。