与Lorenz曲线相关的指标

15 Jul 2016

在前面一篇博客“对加权Gini系数的理解”中，我们已经对Lorenz曲线的构造方法进行了探讨，当时的主要目的是计算加权Gini系数。事实上，Gini系数并不能表现出Lorenz曲线的全部信息，因为同一个Gini系数可能对应不同的Lorenz曲线。为了进一步挖掘Lorenz曲线的信息，Damgaard等人¹提出了Lorenz不对称系数，用来说明不公平性到底是由于低收入的人群占比太高导致的，还是由于少量人群占据了大量的收入所致。另外，学者还提出了Hoover指数(或者称为Ricci-Schutz系数以及Robin Hood指数)，用来分析到底有多大比例的收入需要再分配才能实现“绝对公平”。由于Hoover指数相对比较简单，这里先探讨Hoover指数，然后再对Lorenz不对称系数进行说明。

1 Hoover指数

Hoover指数的想法是十分简单的，假设有$n$个人的收入分别为$x_1,x_2,\cdots,x_n$，其平均数为$\bar{x}$，考虑到最公平的分配方式是这$n$个人的收入都是$\bar{x}$，那么每个人的缺口就是$\|x_i-\bar{x}\|$。这时我们可以计算出总的缺口占总收入的比例：

$$\text{HI}=\dfrac{\sum_{i=1}^n\|x_i-\bar{x}\|}{2\sum_{i=1}^n{x_i}}$$

这个比例就是Hoover指数。在Hoover指数的计算公式中需要除以$2$，其原因是$x_i-\bar{x}<0$的$\|x_i-\bar{x}\|$的总和与$x_i-\bar{x}>0$的$\|x_i-\bar{x}\|$的总和相等，也就是说高于平均收入的人群需要拿出的收入的总和等于低于平均收入的人群需要获得的收入的总和时才能实现“绝对公平”。按照这种方式，我们很容易就能计算出“对加权Gini系数的理解”中第一个表格中数据的Hoover指数，其结果为 $0.206$。

以上计算过程似乎与Lorenz曲线没有任何关系，而实际上通过Lorenz曲线我们同样可以得到相同的结果。对于Lorenz曲线，我们可以对曲线上每一点作$x$轴的垂线，该垂线与Lorenz曲线和绝对公平线(对角线)相交所得线段长度中最长的那个线段的长度刚好就是上面计算的$0.206$(过该点作对角线的平行线不与Lorenz曲线相交)。由此可见，Hoover指数还可以写成另外一种关于$F(x)$和$L(x)$的表达式：

$$\text{HI}=\max_x\{F(x)-L(x)\}$$

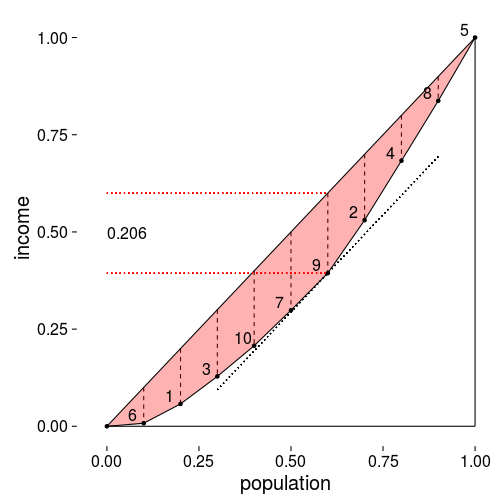
难以想象以上两种计算方法竟然是等效的。下面就对这种等效性进行说明。从“对加权Gini系数的理解”中我们知道$F(x_{h}^{\prime})=\sum_{i=0}^{h}w_{i}^{\prime}/\sum_{i=0}^{n}w_{i}^{\prime}$和 $L(x_{h}^{\prime})=\sum_{i=0}^{h}z_{i}^{\prime}/\sum_{i=0}^{n}z_{i}^{\prime}$，并且有$z_{i-1}^{\prime}/w_{i-1}^{\prime}<z_{i}^{\prime}/w_{i}^{\prime}$，同时，我们假设Lorenz曲线上第$i$个点与第$i-1$个点的连线的斜率为$k_i$，那么有

$$k_i=\dfrac{z_{i}^{\prime}/\sum_{i=0}^{n}z_{i}^{\prime}}{w_{i}^{\prime}/\sum_{i=0}^{n}w_{i}^{\prime}}$$

很明显，$k_{i-1}<k_{i}$且$k_i>0$。另外，对于$F(x_{h}^{\prime})$和$L(x_{h}^{\prime})$，我们记$\mathcal{H}_0^h=F(x_{h}^{\prime})-L(x_{h}^{\prime})$，$H_i^{*}=w_{i}^{\prime}/\sum_{i=0}^{n}w_{i}^{\prime}-z_{i}^{\prime}/\sum_{i=0}^{n}z_{i}^{\prime}$，那么有

$$\mathcal{H}_t^h=\sum_{i=t}^{h}H_i^{*}$$

这里$H_{i-1}^{*}>H_i^{*}$。当$0<k_i<1$时，$H_i^{*}>0$；当$k_i>1$时，$H_i^{*}<0$。由于$H_i^{*}$是递减数列，所以当$H_m^{*}=0$时，$\mathcal{H}_0^m=\sum_{i=0}^{m}H_i^{*}$取到最大值(当$h=m$的时候)。另外，由于$\mathcal{H}_0^n=\mathcal{H}_0^m+\mathcal{H}_{m+1}^n=0$(这个根据定义式可以得到)，所以$\mathcal{H}_0^m=\sum_{i=0}^{n}\|H_i^{*}\|/2$。将$H_i^{*}$的定义式带入后可以得到：

$$\text{HI}=\dfrac{1}{2}\sum_{i=0}^{n}\left\|\dfrac{w_{i}^{\prime}}{\sum_{i=0}^{n}w_{i}^{\prime}}-\dfrac{z_{i}^{\prime}}{\sum_{i=0}^{n}z_{i}^{\prime}}\right\|$$

上式不涉及到排序的问题(即任意一个$w_{i}^{\prime}$都存在一个$w_j$与之对应，在求和上是不用考虑顺序的)，所以可以进一步简化为

$$\text{HI}=\dfrac{1}{2}\sum_{i=0}^{n}\left\|\dfrac{w_i}{\sum_{i=0}^{n}w_i}-\dfrac{z_i}{\sum_{i=0}^{n}z_i}\right\|$$

对“对加权Gini系数的理解”中的第一个例子，我们可以按照$x_{i}^{\prime}$从小到大的顺序依此作出$\mathcal{H}_0^i$和$H_i^{*}$的变化情况。从图中可以看出，当$i=9$的时候，$\mathcal{H}_0^i$达到最大值，同时$H_i^{*}>0$且$H_{i+1}^{*}<0$。

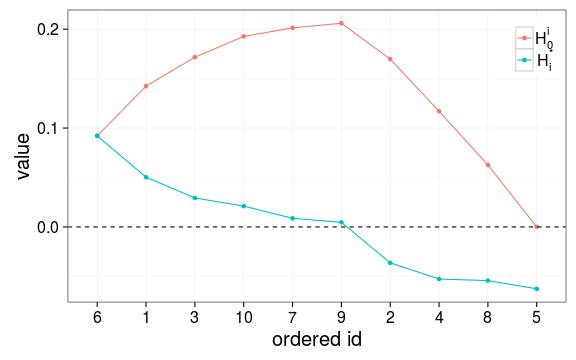
有了这个公式后，我们就很容易求解出加权情况下的Hoover指数。以对“对加权Gini系数的理解”中的第二个例子为例，我们计算的结果为 $0.3048$。

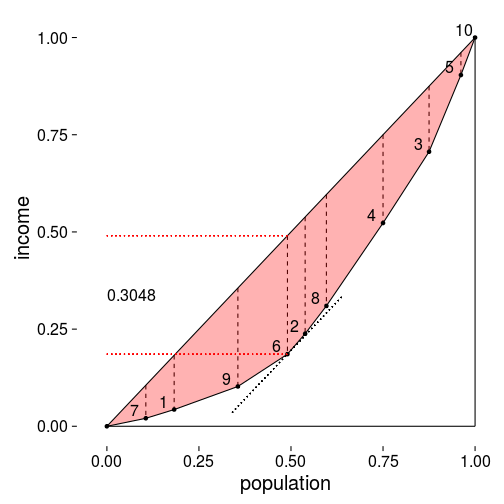
从上面的分析中可以看出，Hoover指数是对Gini系数的一个补充。我们可以构造出两个Gini系数完全相同，但Hoover指数却不一样的数据序列；同样我们也可以构造出两个Hoover指数完全相同，但Gini系数却不一样的数据序列。这表明了，即便是同样多的财富需要再分配才能实现“绝对公平”，但由于其分配方式的不同，所体现出来的公平性是有差别的。

2 Lorenz不对称系数

Lorenz不对称系数(Lorenz asymmetry coefficient)是一个很有意思的指标，它从Lorenz曲线的形状入手来看Lorenz曲线是否关于$x+y=1$这条直线对称。如果不对称，那表征对称性的那个点是在直线上方还是下方？如果在上方，说明少量人群占据了大量的资源；如果在下方，则说明资源拥有量少的人群占比太高。那么如何找到这个表征对称性的点呢？其实，如果我们假设Lorenz曲线关于$x+y=1$这条直线对称，那么过它与这条直线的交点作Lorenz曲线的切线，这条切线将平行于$x-y=0$这条直线(即绝对公平线)。那么从本文的第一部分中，我们就知道了在Lorenz曲线上平行于绝对公平线的切线上的切点是一个十分重要的点，Hoover指数就定义为该点与绝对公平线的垂向距离(垂直于$x$轴)。为了说明该点的性质，我们还是从 $F(x)$和$L(x)$的定义说起。

$$\begin{cases} F(x)=\int_{0}^{x}\text{d}F(t)\\ L(x)=\int_{0}^{x}t\text{d}F(t)/\mu \end{cases}$$

其中$\mu=\int_{0}^{+\infty}t\text{d}F(t)$，为随机变量$X$的期望值。如果我们令$p=F(x)$，那么$L(x)$可以写成关于$p$的函数：

$$L(p)=\dfrac{1}{\mu}\int_0^pF^{-1}(t)\text{d}t$$

对$L(p)$求导可以得到：

$$\dfrac{\text{d}L(p)}{\text{d}p}=\dfrac{F^{-1}(p)}{\mu}$$

当平行于绝对公平线时，$L^{\prime}(p)=1$，也就是说$F^{-1}(p)=\mu$，或者$p=F(\mu)$，或者$x=\mu$。由此可见，这一切点的坐标为$(F(\mu),L(\mu))$。这样问题就变得明朗了：如果Lorenz曲线对称，那么$(F(\mu),L(\mu))$就在直线$x+y=1$上，也就是说$F(\mu)+L(\mu)=1$。那么就可有定义一个称为Lorenz不对称系数的指标：

$$\text{LAC}=F(\mu)+L(\mu)$$

当$\text{LAC}>1$时，点$(F(\mu),L(\mu))$在直线$x+y=1$上方，说明少量人群占据了大量的资源；当$\text{LAC}<1$时，点$(F(\mu),L(\mu))$在直线$x+y=1$下方，则说明资源拥有量少的人群占比太高。

$\text{LAC}$的计算方法似乎很简单，我们很容易得到$\mu$的值，然后我们只需要按照“对加权Gini系数的理解”中的方法构造 $F(x)$和$L(x)$曲线，代入$\mu$的值即可以算出。理论很完美，但实际分析过程中我们并没有连续性的假设，所用的数据都是离散的点，而$\mu$往往也不在散点上。为此Damgaard等人¹针对非加权条件下的数据(实际上可以看成是加权数据)采用内插法提供了一套计算思路：

$$\begin{cases} \delta=\dfrac{\hat{\mu}-x_{m}^{\prime}}{x_{m+1}^{\prime}-x_{m}^{\prime}}\\ F(\hat{\mu})=\dfrac{m+\delta}{n}\\ L(\hat{\mu})=\dfrac{L_{m}+\delta x_{m+1}^{\prime}}{L_{n}} \end{cases}$$

以他文中提出的算例为例，我们按照非加权与加权两种方式来看采用内插法得到的$F(x)$的结果(如下图)。从图中可以很明显地看到，对于非加权与加权两种方式而言，只有在比较特殊的条件下，二者能有一致的结果，否者求出来的$p$值差别很大。在这种情况下，本文建议直接采用传统的阶梯函数的形式对$F(x)$和$L(x)$进行估计，这样得到的结果对于非加权与加权两种方式就是一致的。

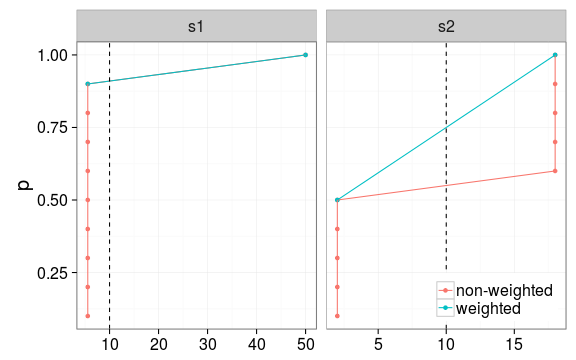
采用上述思路对于s1和s2计算出来的$\text{LAC}$分别为$1.4$和$0.6$，而原文计算出来的结果分别为$1.46$和$0.74$。相比较而言，两种算法的结果差别不大，对最终的结论没有影响。但是本文提供的算法刚好捕捉到的是s1和s2在Lorenz曲线上突出的那点，故本文认为采用阶梯函数估值要比内插法估值更为稳健和可靠。

参考文献