基于泰勒展开的不确定性传递
07 Oct 20161 两个输入变量
假设随机变量是随机变量和随机变量的函数,函数关系如下
其中和的均值分别为和,方差分别为1和,协方差为。对进行关于和泰勒展开可以得到
如果忽略高阶项,那么根据随机变量求和的期望和方差计算公式
和
可以得到的期望值与方差值分别如下
和
如果我们对、和取对数,那么理论上存在
根据泰勒展开公式,有
其中
这里表示参数的相对敏感性系数(类似于经济学中的弹性系数)2。根据以上推导可以得到的期望值与方差值分别如下
和
2 多个输入变量
对于更一般的情况,假设是变量的函数
同时有
那么的期望值与方差值分别如下
和
以及的期望值与方差值分别如下
和
3 举个例子
假设随机变量与随机变量和随机变量满足如下的函数关系
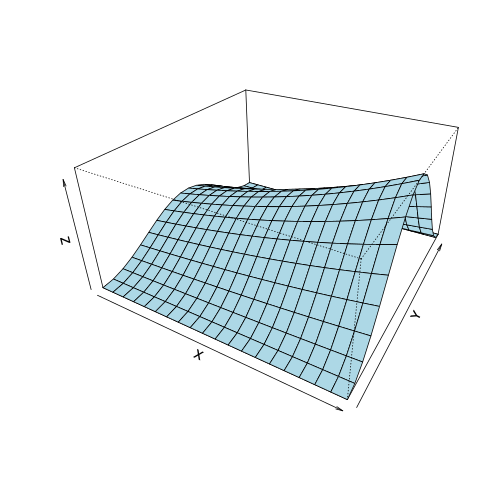
这里,,并且和互相独立。分别将对和求导,可以得到
和
另外,对于,有
和
那么有,,,。则的期望值与方差值的计算结果分别如下
和
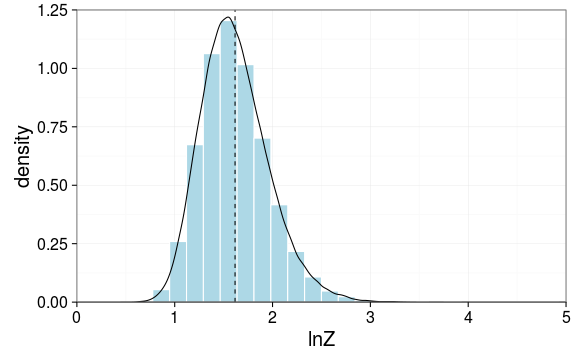
如果采用Monte Carlo随机模拟,估算出的,。
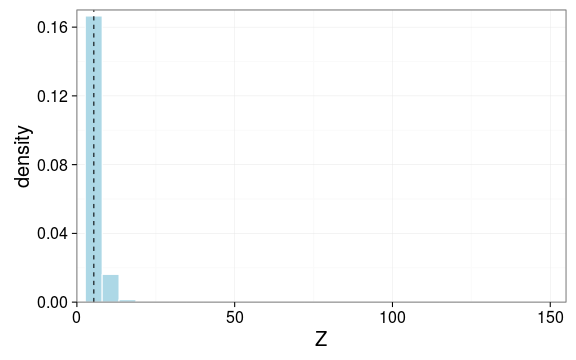
另外,的期望值与方差值的计算结果分别如下
和
如果采用Monte Carlo随机模拟,估算出的,。